
Numeri fracti по-русски


Википедия Черепнин Л.В. Русская метрология Цифирь: как на Руси учились считать до Петра Великого Бобынин В. В. Очерки истории развития физико-математических знаний в России. Вып. 2. — 1893 Древнерусская вычислительная практика Счет костьми и дощаный счет









двоичный ряд дробей, построенный из дроби 1/2 и ее "производных" (половина, четь, пол-чети и т.д.); двоично-троичный ряд дробей, построенный из дроби 1/3 и ее "производных" (треть, пол-треть, пол-пол-треть и т.д.).








К приемам, используемым в сошной арифметике, относятся "счет костьми" и "дощаный счет", а основным инструментом - "Дщица счетная", прибор для дощаного счета. Более подробно об этом можно прочитать здесь.
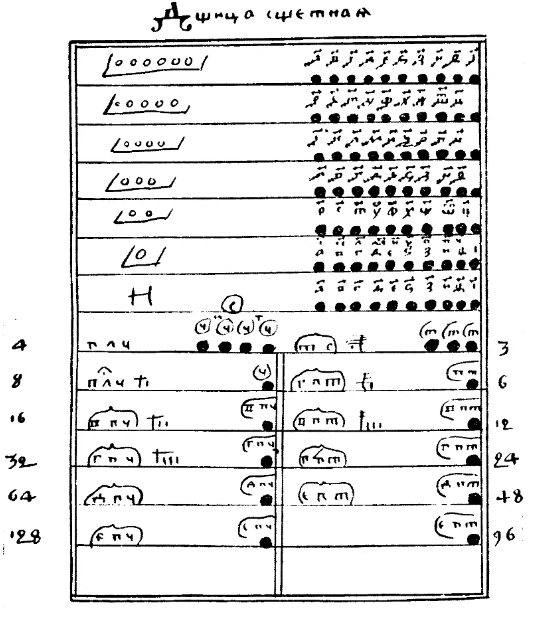
Информацию о рукописи можно найти в книге Бобынина В. В. «Очерки истории развития физико-математических знаний в России», Вып. 2. — 1893. Она представляет собой таблицу сумм, получаемых при сложении различных частей сохи. Практическая значимость равенств в данной таблице состояла в переводе одних сошных дробей в другие, что было нужно для рационализации вычислений при взимании налога с угодий, состоящих из участков владений различной величины и ценности (пашни, леса, луга и пр.). Кроме этой рукописи существовало много правил «Свода мелких костей», т.е. сложения употребительных в сошном счете дробей, вроде «три чети сохи да полчети сохи да полполчети сохи» и т.д. вплоть до «пол-пол-пол-пол-полчети сохи составляют соху без пол-пол-пол-пол-полчети», т.е. 3/4+1/8+1/16+1/32 +1/64 + 1/128 = 1 - 1/128 и т.п.
Соха – условная мера, в данных правилах принимается за 1. Проанализировав все правила, приводимые в этой таблице, мы получили следующее (синей ручкой выделены верные примеры, красной – неверные; неверные затем исправлены) (см.галерею).
Соха – условная мера, в данных правилах принимается за 1. Проанализировав все правила, приводимые в этой таблице, мы получили следующее (синей ручкой выделены верные примеры, красной – неверные; неверные затем исправлены) (см.галерею).
Далее мы предлагаем свои примеры на именование современных дробей согласно древнерусским правилам:

- Сложение двух одинаковых «сошных» дробей дает дробь ближайшего высшего разряда.
- Дроби суммировались без приведения к общему знаменателю.
- В сошной арифметике результаты имели точность до 1/48. Если же в итоге получались более мелкие дроби, то их попросту отбрасывали, полагая, что их учет не повлияет по существу на результат.
Особенности сошной арифметики
